三角形の垂心計算機

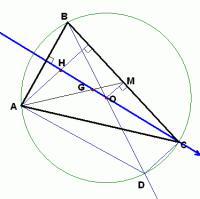
⊿ABCの3つの高さをAD、BE、CFとし、そのうちD、E、Fを垂線の足とし、垂心をHとする。角A、B、Cの対辺はそれぞれa、b、c

1. 鋭角三角形の垂心は三角形の内側にあります。直角三角形の垂心は直角の頂点にあります。鈍角三角形の垂心は三角形の外側にあります。

2. 三角形の垂心は、その垂直三角形の内心です。または、三角形の内心は、その傍心三角形の垂心です。 3. 垂心Hの3辺についての対称点はすべて△ABCの外接円上にある。

4. △ABCには、共円となる4点のグループが6つあり、相似な直角三角形のグループが3つ（各グループに4つ）あり、AH·HD=BH·HE=CH·HFです。

5. H、A、B、C のいずれかの点は、他の 3 点を頂点とする三角形の垂心です (このような 4 点は垂心群と呼ばれます)。

6. △ABC、△ABH、△BCH、△ACHの外接円は等しい円です。

7. 直角でない三角形では、H を通る直線が直線 AB および直線 AC とそれぞれ P および Q で交差するため、AB/AP·tanB+AC/AQ·tanC=tanA+tanB+tanC となります。

8. 三角形の任意の頂点から垂心までの距離は、外心から反対側の辺までの距離の 2 倍に等しくなります。

9. △ABCの外心と垂心をそれぞれOとHとすると、∠BAO=∠HAC、∠ABH=∠OBC、∠BCO=∠HCAとなる。

10. 鋭角三角形の垂心からその 3 つの頂点までの距離の合計は、その内接円と外接円の半径の合計の 2 倍に等しくなります。

11. 鋭角三角形の垂心は、底三角形の内心です。鋭角三角形に内接する三角形（頂点が元の三角形の辺上にある三角形）の中で、底三角形の周囲が最も短くなります。

12. シムソンの定理（シムソン線）：ある点から三角形の 3 辺に引いた垂線の足が同一直線になるための必要かつ十分な条件は、その点が三角形の外接円上にあることです。

13. 鋭角⊿ABCの内側に点Pがあるとすると、Pが垂心となるための必要十分条件はPB*PC*BC+PB*PA*AB+PA*PC*AC=ABである。 *BC*CA。