Desetinná desetinná část o kalkulačce trvalého zlomku

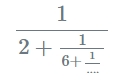
Co je to kalkulačka desetinných až spojitých zlomků?

Kalkulačka desetinných míst na nepřetržitý zlomek je nástroj, který převádí desetinné číslo (číslo se základem 10) do tvaru pokračujícího zlomku. Nepřetržitý zlomek je reprezentace čísla jako celá část plus řada zlomků, které umožňují přesnější a kompaktnější reprezentace reálných čísel. Tento formulář je zvláště užitečný pro aproximaci iracionálních čísel.

Proč používat kalkulačku desetinných až pokračujících zlomků?

• Přesná aproximace: Je to účinný způsob, jak aproximovat iracionální čísla pomocí konečných zlomků, se kterými se snadněji manipuluje při výpočtech.
• Aplikace teorie čísel: Pokračující zlomky se používají v teorii čísel ke studiu iracionálních čísel, diofantických rovnic a aproximaci odmocnin nebo jiných iracionálních čísel.
• Matematická analýza: Užitečné při analýze konvergence sekvencí nebo řad v oborech, jako je teorie aproximace, kryptografie a výpočetní matematika.
• Efektivní znázornění iracionálních čísel: Iracionální čísla, jako je π nebo e, mají nekonečná desetinná rozšíření. Pokračující zlomky poskytují efektivnější a užitečnější způsob vyjádření a aproximace těchto čísel.
• Zjednodušuje složité výpočty: V určitých kontextech poskytují spojité zlomky srozumitelnější vyjádření čísel, díky čemuž jsou výpočty s nimi snazší a efektivnější.

Jak funguje kalkulačka desetinných a nepřetržitých zlomků?

1. Zadejte desetinné číslo:
   • Zadejte desetinné číslo, které chcete převést na jeho pokračující zlomek.
2. Použití konverze: Kalkulačka:
   • Rozdělte desetinné číslo na jeho celočíselnou část a zlomkovou část.
   • Jako první člen pokračovacího zlomku použijte část celého čísla.
   • Opakujte postup pro zlomkovou část a pokračujte v hledání celé části převrácené hodnoty zlomkového zbytku.
   • Pokračujte, dokud nedosáhnete požadované úrovně přesnosti nebo dokud se pokračovací zlomek plně nerozšíří.

Kdy použít kalkulačku desetinných až pokračujících zlomků?

• V teorii čísel: Při práci s racionálními aproximacemi iracionálních čísel nebo při studiu diofantických rovnic.
• Pro aproximaci iracionálních čísel: Při práci s iracionálními čísly, jako je π, e nebo odmocniny, představují spojité zlomky způsob, jak je aproximovat efektivněji.
• V kryptografii: Některé šifrovací algoritmy používají pokračující zlomky k prolomení kódů nebo v algoritmických přístupech k teorii čísel.
• V matematickém výzkumu: Výzkumníci v oborech, jako je algebraická teorie čísel, používají spojité zlomky k řešení problémů zahrnujících reálná čísla a iracionální konstanty.
• V nastavení pro vzdělávání: Při studiu číselných soustav, iracionálních čísel nebo teorie aproximací mohou pokračující zlomky studentům pomoci pochopit, jak lze reálná čísla znázornit ve srozumitelnější podobě.