ทศนิยมถึงเครื่องคิดเลขเศษส่วนต่อเนื่อง

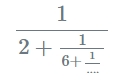
เครื่องคิดเลขทศนิยมต่อเศษส่วนต่อเนื่องคืออะไร

a ทศนิยมไปยังเครื่องคิดเลขเศษส่วนต่อเนื่อง เป็นเครื่องมือที่แปลงตัวเลขทศนิยม (ตัวเลขในฐาน 10) เป็นค่าสัดส่วน ต่อเนื่อง เศษส่วนอย่างต่อเนื่องคือการเป็นตัวแทนของตัวเลขเป็นส่วนจำนวนเต็มบวกชุดของเศษส่วนที่อนุญาตให้มีการเป็นตัวแทนที่แม่นยำและกะทัดรัดมากขึ้นของจำนวนจริง แบบฟอร์มนี้มีประโยชน์อย่างยิ่งสำหรับการประมาณจำนวนที่ไม่มีเหตุผล

ทำไมต้องใช้เครื่องคิดเลขทศนิยมกับเศษส่วนต่อเนื่อง?

• การประมาณที่แม่นยำ: เป็นวิธีที่มีประสิทธิภาพในการประมาณจำนวนที่ไม่มีเหตุผลโดยมีเศษส่วนอย่างต่อเนื่อง จำกัด ซึ่งง่ายต่อการจัดการในการคำนวณ
• แอพพลิเคชั่นทฤษฎีจำนวน: ใช้เศษส่วนต่อเนื่องในทฤษฎีจำนวนสำหรับการศึกษาตัวเลขที่ไม่มีเหตุผล, Dสมการ iophantine และประมาณรากสี่เหลี่ยมหรือตัวเลขที่ไม่มีเหตุผลอื่น ๆ
• การวิเคราะห์ทางคณิตศาสตร์: มีประโยชน์ในการวิเคราะห์การบรรจบกันของลำดับหรือซีรีส์ในสาขาเช่นทฤษฎีการประมาณการเข้ารหัสและคณิตศาสตร์เชิงคำนวณ
• การเป็นตัวแทนที่ไม่มีเหตุผล: จำนวนที่ไม่มีเหตุผลเช่นπหรือ E มีการขยายทศนิยมที่ไม่มีที่สิ้นสุด เศษส่วนอย่างต่อเนื่องให้วิธีที่มีประสิทธิภาพและมีประโยชน์มากขึ้นในการแสดงและประมาณตัวเลขเหล่านี้
• ทำให้การคำนวณที่ซับซ้อนง่ายขึ้น: ในบริบทบางอย่างเศษส่วนอย่างต่อเนื่องให้การแสดงออกของตัวเลขที่จัดการได้มากขึ้นทำให้การคำนวณที่เกี่ยวข้องกับพวกเขาง่ายขึ้นและมีประสิทธิภาพมากขึ้น

เครื่องคิดเลขทศนิยมไปยังส่วนต่อเนื่องได้อย่างไร?

1. ป้อนหมายเลขทศนิยม:
   • ป้อนหมายเลขทศนิยมที่คุณต้องการแปลงเป็นแบบฟอร์มเศษส่วนอย่างต่อเนื่อง
2. ใช้การแปลง: เครื่องคิดเลขจะ:
   • แบ่งหมายเลขทศนิยมออกเป็นส่วนจำนวนเต็มและส่วนที่เป็นเศษส่วน
   • ใช้ส่วนจำนวนเต็มเป็นเทอมแรกของส่วนต่อเนื่อง
   • ทำซ้ำกระบวนการสำหรับส่วนที่เป็นเศษส่วนอย่างต่อเนื่องเพื่อค้นหาส่วนจำนวนเต็มของส่วนซึ่งกันและกันของเศษส่วนที่เหลืออยู่
   • ดำเนินการต่อไปจนกว่าจะถึงระดับความแม่นยำที่ต้องการหรือส่วนต่อเนื่องจะขยายออกอย่างเต็มที่

เมื่อใดควรใช้ทศนิยมกับเครื่องคิดเลขเศษส่วนต่อเนื่อง?

• ในทฤษฎีจำนวน: เมื่อทำงานกับการประมาณเหตุผลของตัวเลขที่ไม่มีเหตุผลหรือในการศึกษาสมการ diophantine
• สำหรับการประมาณจำนวนที่ไม่มีเหตุผล: เมื่อต้องรับมือกับตัวเลขที่ไม่มีเหตุผลเช่นπ, E หรือรากสี่เหลี่ยมจัตุรัสส่วนต่อเนื่องเป็นวิธีที่จะประมาณพวกเขาได้อย่างมีประสิทธิภาพมากขึ้น
• ในการร้องไห้Ptography: อัลกอริธึมการเข้ารหัสบางอย่างใช้เศษส่วนอย่างต่อเนื่องสำหรับการทำลายรหัสหรือในวิธีการอัลกอริทึมในทฤษฎีจำนวน
• ในการวิจัยทางคณิตศาสตร์: นักวิจัยในสาขาเช่นทฤษฎีตัวเลขพีชคณิตใช้เศษส่วนอย่างต่อเนื่องเพื่อแก้ปัญหาที่เกี่ยวข้องกับจำนวนจริงและค่าคงที่ไม่มีเหตุผล
• ในการตั้งค่าการศึกษา: เมื่อศึกษาระบบตัวเลขตัวเลขที่ไม่มีเหตุผลหรือทฤษฎีการประมาณค่าเศษส่วนอย่างต่อเนื่องสามารถช่วยให้นักเรียนเข้าใจว่าจำนวนจริงสามารถแสดงได้อย่างไรในรูปแบบที่จัดการได้มากขึ้น