小数到连分数计算器
输入值并单击计算。将显示结果。
公式:
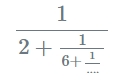
什么是小数转连分数计算器?
小数转连分数计算器是一种将十进制数(十进制数)转换为连分数形式的工具。连分数是将数字表示为整数部分加上一系列分数,从而可以更精确、更紧凑地表示实数。这种形式对于近似无理数特别有用。
为什么使用小数到连分数计算器?
- 精确近似:用有限连分数近似无理数是一种有效的方法,在计算中更容易处理。
- 数论应用:连分数在数论中用于研究无理数、丢番图方程以及近似平方根或其他无理数。
- 数学分析:在近似理论、密码学和计算数学等领域中,可用于分析序列或级数的收敛性。
- 无理数的有效表示:无理数,例如π或e,具有无限十进制扩展。连分数提供了一种更有效、更有用的表达和近似这些数字的方法。
- 简化复杂计算:在某些情况下,连分数提供了更易于管理的数字表达,使涉及它们的计算更容易、更高效。
小数到连分数计算器如何工作?
- 输入小数:
- 输入要转换为连分数形式的小数。
- 应用转换:计算器将:
- 将小数分解为整数部分和小数部分。
- 使用整数部分作为连分数的第一项。
- 对小数重复该过程小数部分,继续求小数余数的倒数的整数部分。
- 继续,直到达到所需的精度,或者连分数完全展开。
何时使用小数到连分数计算器?
- 在数论中:处理无理数的有理近似值时,或在研究丢番图方程时。
- 用于近似无理数:处理无理数(如π、e 或平方根)时,连分数提供了一种更有效地近似它们的方法。
- 在密码学中:一些加密算法使用连分数来破译密码或用于数论的算法方法。
- 在数学研究中:代数数论等领域的研究人员使用连分数来解决涉及实数和无理常数的问题。
- 在教育设置:在学习数字系统、无理数或近似理论时,连分数可以帮助学生理解如何以更易于管理的形式表示实数。
此计算器对您有帮助吗?
感谢您的反馈


搜索计算器
探索全球数百万人信赖的数千款免费计算器.