Decimal til fortsat fraktionsregnement

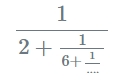
Hvad er en decimal til fortsat brøkberegner?

En Decimal til fortsat brøkberegner er et værktøj, der konverterer et decimaltal (et tal i grundtallet 10) til dets fortsatte brøk-form. En fortsat brøk er en repræsentation af et tal som en heltalsdel plus en række brøker, der giver mulighed for mere præcise og kompakte repræsentationer af reelle tal. Denne formular er især nyttig til at tilnærme irrationelle tal.

Hvorfor bruge en decimal til fortsat brøkberegner?

• Nøjagtig approksimation: Det er en effektiv måde at tilnærme irrationelle tal med endelige fortsatte brøker, som er nemmere at håndtere i beregninger.
• Anvendelser for talteori: Fortsatte brøker bruges i talteori til at studere irrationelle tal, diofantiske ligninger og tilnærmelse af kvadratrødder eller andre irrationelle tal.
• Matematisk analyse: Nyttig til at analysere konvergensen af ​​sekvenser eller serier inden for felter som tilnærmelsesteori, kryptografi og beregningsmatematik.
• Effektiv repræsentation af irrationale: Irrationelle tal, såsom π eller e, har uendelige decimaludvidelser. Fortsatte brøker giver en mere effektiv og nyttig måde at udtrykke og tilnærme disse tal på.
• Forenkler komplekse beregninger: I visse sammenhænge giver fortsatte brøker mere håndterbare udtryk for tal, hvilket gør beregninger, der involverer dem, nemmere og mere effektive.

Hvordan virker en decimal til fortsat brøkberegner?

1. Indtast decimaltallet:
   • Indtast det decimaltal, du vil konvertere til dets fortsatte brøkform.
2. Anvend konverteringen: Lommeregneren vil:
   • Opdel decimaltallet i dets heltalsdel og brøkdel.
   • Brug heltalsdelen som det første led i den fortsatte brøk.
   • Gentag processen for brøkdelen, fortsæt med at finde den heltallige del af den reciproke del af brøkresten.
   • Fortsæt, indtil det ønskede præcisionsniveau er nået, eller den fortsatte fraktion er fuldt udvidet.

Hvornår skal man bruge en decimal til fortsat brøkberegner?

• I talteori: Når man arbejder med rationelle tilnærmelser af irrationelle tal, eller i studiet af diofantiske ligninger.
• Til tilnærmelse af irrationelle tal: Når man har at gøre med irrationelle tal som π, e eller kvadratrødder, giver fortsatte brøker en måde at tilnærme dem mere effektivt.
• I kryptografi: Nogle krypteringsalgoritmer bruger fortsatte brøker til at bryde koder eller i algoritmiske tilgange til talteori.
• I matematisk forskning: Forskere inden for områder som algebraisk talteori bruger fortsatte brøker til at løse problemer, der involverer reelle tal og irrationelle konstanter.
• I uddannelsesindstillinger: Når man studerer talsystemer, irrationelle tal eller tilnærmelsesteorien, kan fortsatte brøker hjælpe eleverne med at forstå, hvordan reelle tal kan repræsenteres i en mere overskuelig form.