Decimaal tot voortdurende breukcalculator

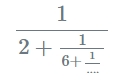
Wat is een decimaal tot voortdurende fractiecalculator?

a decimaal tot vervolg fractiecalculator is een hulpmiddel dat een decimaal getal (een getal in basis 10) omzet in zijn vervolg fractie vorm. Een voortdurende fractie is een weergave van een getal als gehele onderdeel plus een reeks breuken die meer precieze en compacte representaties van reële getallen mogelijk maken. Deze vorm is vooral handig voor het benaderen van irrationele getallen.

Waarom een ​​decimaal gebruiken tot voortdurende fractiecalculator?

• Nauwkeurige benadering: Het is een efficiënte manier om irrationele getallen te benaderen met eindige voortdurende breuken, die gemakkelijker te hanteren zijn in berekeningen.
• Nummertheorietoepassingen: Voortgezette breuken worden gebruikt in getaltheorie voor het bestuderen van irrationele getallen, Diophantine equations, and approximating square roots or other irrational numbers.
• Wiskundige analyse: nuttig bij het analyseren van de convergentie van sequenties of series in velden zoals benaderingtheorie, cryptografie en computationele wiskunde.
• Efficiënte weergave van irrationals: irrationele getallen, zoals π of E, hebben oneindige decimale uitbreidingen. Voortgezette breuken bieden een efficiëntere en nuttiger manier om deze cijfers uit te drukken en te benaderen.
• vereenvoudigt complexe berekeningen: In bepaalde contexten bieden voortdurende breuken meer beheersbare uitingen van getallen, waardoor berekeningen worden betrokken bij hen gemakkelijker en efficiënter.

Hoe werkt een decimaal tot vervolg fractiecalculator?

1. voer het decimale nummer in:
   • Voer het decimale nummer in dat u wilt converteren in zijn voortdurende breukvorm.
2. Pas de conversie toe: De rekenmachine zal:
   • Breek het decimale nummer in zijn gehele onderdeel en fractionele deel.
   • Gebruik het gehele onderdeel als de eerste term van de voortdurende fractie.
   • Herhaal het proces voor het fractionele gedeelte en blijf het gehele onderdeel van de wederzijdse van de fractionele rest vinden.
   • Ga door totdat het gewenste niveau van precisie is bereikt, of de voortdurende fractie volledig is uitgebreid.

---

Wanneer een decimaal te gebruiken tot vervolg fractiecalculator?

• in getallentheorie: Bij het werken met rationele benaderingen van irrationele getallen, of in de studie van diofantijnse vergelijkingen.
• Voor het benaderen van irrationele getallen: bij het omgaan met irrationele getallen zoals π, E of vierkante wortels, bieden voortdurende breuken een manier om ze efficiënter te benaderen.
• in huilPTOGRAFIE: Sommige coderingsalgoritmen gebruiken voortdurende breuken voor het breken van codes of in algoritmische benaderingen van getaltheorie.
• in wiskundig onderzoek: onderzoekers in velden zoals algebraïsch aantal theorie gebruiken voortdurende breuken om problemen op te lossen met reële getallen en irrationele constanten.
• In educatieve instellingen: Bij het bestuderen van getallensystemen, irrationele getallen of de theorie van benaderingen, kunnen voortdurende breuken studenten helpen begrijpen hoe reële getallen in een beter beheersbare vorm kunnen worden weergegeven.