小数から連分数への計算機

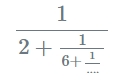
小数から連分数への変換計算機とは何ですか?

小数から連分数への変換計算機は、小数 (10 進数) を 連分数 形式に変換するツールです。連分数とは、整数部分と一連の分数で表した数値表現で、実数をより正確かつ簡潔に表現できます。この形式は、無理数を近似するのに特に便利です。

小数から連分数への計算機を使用する理由

• 正確な近似: 有限連分数で無理数を近似する効率的な方法であり、計算で扱いやすくなります。
• 数論の応用: 連分数は、無理数、ディオファントス方程式の研究、および平方根やその他の無理数の近似に数論で使用されます。
• 数学的分析: 近似理論、暗号学、計算数学などの分野で、シーケンスまたはシリーズが収束するのを分析するのに役立ちます。
• 無理数の効率的な表現: π や e などの無理数は、無限の小数展開を持ちます。連分数は、これらの数値をより効率的かつ便利に表現し、近似値を求める方法を提供します。
• 複雑な計算を簡素化: 特定の状況では、連分数は数値をより扱いやすい表現にし、連分数を含む計算をより簡単に、より効率的にします。

小数から連分数への計算機はどのように機能しますか?

1. 小数を入力します:
   • 連分数形式に変換する小数を入力します。
2. 変換を適用します: 計算機は次の操作を行います:
   • 小数を整数部分と小数部分に分割します。
   • 整数部分を連分数の最初の項として使用します。
   • 小数部分に対してこのプロセスを繰り返し、分数剰余の逆数の整数部分を見つけます。
   • 必要な精度レベルに達するか、連分数が完全に展開されるまで続けます。

小数から連分数への計算機はいつ使うべきでしょうか?

• 数論:無理数の有理近似を扱うとき、またはディオファントス方程式の研究で。
• 無理数の近似:π、e、平方根などの無理数を扱うとき、連分数はより効率的に近似する方法を提供します。
• 暗号化:一部の暗号化アルゴリズムは、コードを解読するため、または数論へのアルゴリズム的アプローチで連分数を使用します。
• 数学研究:代数的数論などの分野の研究者は、実数と無理定数を含む問題を解決するために連分数を使用します。
• 教育環境: 数体系、無理数、近似理論を学ぶ際、連分数は、実数を扱いやすい形式で表現する方法を学生が理解するのに役立ちます。