Decimal till fortsatt fraktionskalkylator

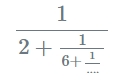
Vad är en kalkylator för decimaler till fortsatt bråk?

En decimal till fortsättningsbråkräknare är ett verktyg som konverterar ett decimaltal (ett tal i bas 10) till dess fortsatta bråk-form. Ett fortsatt bråk är en representation av ett tal som en heltalsdel plus en serie bråk som möjliggör mer exakta och kompakta representationer av reella tal. Det här formuläret är särskilt användbart för att approximera irrationella tal.

Varför använda en decimal till fortsättningsbråkräknare?

• Exakt approximation: Det är ett effektivt sätt att approximera irrationella tal med ändliga fortsatta bråk, som är lättare att hantera i beräkningar.
• Talteoritillämpningar: Fortsatta bråk används i talteorin för att studera irrationella tal, diofantiska ekvationer och approximerande kvadratrötter eller andra irrationella tal.
• Matematisk analys: Användbar för att analysera konvergensen av sekvenser eller serier inom områden som approximationsteori, kryptografi och beräkningsmatematik.
• Effektiv representation av irrationer: Irrationella tal, som π eller e, har oändliga decimalexpansion. Fortsatta bråk ger ett mer effektivt och användbart sätt att uttrycka och approximera dessa siffror.
• Förenklar komplexa beräkningar: I vissa sammanhang ger fortsatta bråk mer lätthanterliga uttryck av tal, vilket gör beräkningar som involverar dem enklare och effektivare.

Hur fungerar en decimal-till-fortsättningsbråkräknare?

1. Ange decimaltalet:
   • Ange det decimaltal som du vill konvertera till dess fortsatta bråkform.
2. Tillämpa omvandlingen: Kalkylatorn kommer att:
   • Dela upp decimaltalet i dess heltalsdel och bråkdel.
   • Använd heltalsdelen som den första termen i det fortsatta bråket.
   • Upprepa processen för bråkdelen och fortsätt att hitta heltalsdelen av det reciproka av bråkresten.
   • Fortsätt tills den önskade precisionsnivån har uppnåtts, eller tills den fortsatta fraktionen är helt expanderad.

När ska man använda en decimal-till-fortsättningsbråkräknare?

• I talteorin: När man arbetar med rationella approximationer av irrationella tal, eller när man studerar diofantiska ekvationer.
• För att approximera irrationella tal: När man hanterar irrationella tal som π, e eller kvadratrötter, ger fortsatta bråk ett sätt att approximera dem mer effektivt.
• Inom kryptografi: Vissa krypteringsalgoritmer använder kontinuerliga bråktal för att bryta koder eller i algoritmiska metoder för talteori.
• Inom matematisk forskning: Forskare inom områden som algebraisk talteori använder fortsatta bråktal för att lösa problem som involverar reella tal och irrationella konstanter.
• I utbildningsmiljöer: När man studerar talsystem, irrationella tal eller approximationsteorin kan fortsatta bråk hjälpa eleverna att förstå hur reella tal kan representeras i en mer hanterbar form.