Kalkulačka desatinnej k kalkulačke frakcie

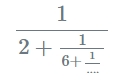
Čo je to desatinná kalkulačka frakcie?

a kalkulačka desatinnej frakcie je nástroj, ktorý prevedie desatinné číslo (číslo v základni 10) do svojej pokračujúcej frakcie . Pokračujúca frakcia je reprezentáciou čísla ako celočíselnej časti plus séria frakcií, ktoré umožňujú presnejšie a kompaktnejšie znázornenie reálnych čísel. Táto forma je užitočná najmä pre aproximovanie iracionálnych čísel.

Prečo používať desatinné miesto na kalkulačku frakcie?

• Presná aproximácia: Je to efektívny spôsob, ako sa približovať iracionálnym číslom s konečnými pokračujúcimi frakciami, ktoré sa pri výpočtoch ľahšie zvládajú.
• Aplikácie teórie čísel: Pokračujúce frakcie sa používajú v teórii čísel na štúdium iracionálnych čísel, Diofantínové rovnice a aproximujúce druhé korene alebo iné iracionálne čísla.
• Matematická analýza: Užitočné pri analýze konvergencie sekvencií alebo sérií v oblastiach, ako je teória aproximácie, kryptografia a výpočtová matematika.
• Efektívne znázornenie iracionálnych: Iracionálne čísla, ako napríklad π alebo e, majú nekonečné desatinné expanzie. Pokračujúce frakcie poskytujú efektívnejší a užitočnejší spôsob vyjadrenia a aproximácie týchto čísel.
• zjednodušuje zložité výpočty: V určitých kontextoch poskytujú pokračujúce frakcie zvládnuteľnejšie vyjadrenia čísel, čo ich uľahčuje a efektívnejšie ich výpočty.

Ako funguje kalkulačka desatinnej frakcie?

1. Zadajte desatinné číslo:
   • Zadajte desatinné číslo, ktoré chcete previesť do svojej formy Frakcie.
2. Použite konverziu: Kalkulačka bude:
   • Rozdeľte desatinné číslo na svoju celú časť a zlomkovú časť.
   • Ako prvé funkčné obdobie pokračujúcej frakcie použite celú časť.
   • Opakujte postup pre frakčnú časť a pokračujte v celej časti recipročného zvyšku frakcie.
   • Pokračujte, kým sa nedosiahne požadovaná úroveň presnosti alebo sa nepretržitá časť úplne rozšíri.

Kedy použiť desatinnú kalkulačku frakcie?

• V teórii čísel: Pri práci s racionálnymi aproximáciami iracionálnych čísel alebo pri štúdiu diofantínskych rovníc.
• Pre aproximovanie iracionálnych čísel: Pri riešení iracionálnych čísel, ako sú π, e alebo odmocniny, pokračujúce frakcie poskytujú spôsob, ako ich efektívnejšie priblížiť.
• v plačuPtografia: Niektoré šifrovacie algoritmy používajú pokračujúce frakcie na prelomenie kódov alebo v algoritmických prístupoch k teórii čísel.
• V matematickom výskume: Vedci v oblastiach, ako je teória algebraických čísel, používať pokračujúce frakcie na riešenie problémov týkajúcich sa skutočných čísel a iracionálnych konštánt.
• Vo vzdelávacích prostrediach: Pri štúdiu číselných systémov, iracionálnych čísel alebo teórie aproximácií môžu pokračujúce frakcie pomôcť študentom pochopiť, ako môžu byť reálne čísla reprezentované v zvládnuteľnejšej forme.