小數到連分數計算器
輸入值並按計算,將顯示結果。
公式:
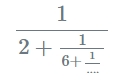
什麼是小數到連分數計算器?
十進位到連分數計算器是一種將十進位數(以 10 為基數的數字)轉換為其連分數形式的工具。連分數是將一個數字表示為一個整數部分加上一系列分數,以便可以更精確、更緊湊地表示實數。這種形式對於近似無理數特別有用。
<小時> 為什麼要用小數到連分數計算器?- 精確近似:用有限連分數來近似無理數是一種有效的方法,在計算中更容易處理。
- 數論應用:連分數在數論中用於研究無理數、丟番圖方程式以及近似平方根或其他無理數。
- 數學分析:有助於分析近似理論、密碼學和計算數學等領域中序列或級數的收斂性。
- 無理數的有效表示:無理數,例如 π 或 e,具有無限小數展開式。連分數提供了一種更有效、更實用的方式來表達和近似這些數字。
- 簡化複雜計算:在某些情況下,連分數提供了更易於管理的數字表達,使涉及它們的計算更容易、更有效率。
- 輸入十進位數:
- 輸入要轉換為連分數形式的十進位數。
- 套用轉換:計算機將:
- 將小數分解為整數部分和小數部分。
- 使用整數部分作為連分數的第一項。
- 對小數部分重複此過程,繼續求小數餘數的倒數的整數部分。
- 繼續,直到達到所需的精度水平,或連分數完全展開。
- 在數論中:在處理無理數的有理近似值或研究丟番圖方程式時。
- 用於近似無理數:在處理諸如 π、e 或平方根之類的無理數時,連分數可以更有效地近似它們。
- 在密碼學中:有些加密演算法使用連分數來破解密碼或採用數論的演算法方法。
- 在數學研究中:代數數論等領域的研究人員使用連分數來解決涉及實數和無理常數的問題。
- 在教育環境中:在學習數字系統、無理數或近似理論時,連分數可以幫助學生理解如何以更易於管理的形式表示實數。
這個計算機對您有幫助嗎?
感謝您的回饋


搜尋計算器
探索全球數百萬人信賴的數千個免費計算器.