Thập phân để tiếp tục máy tính phân số

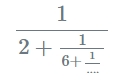
Số thập phân để tiếp tục máy tính phân số là gì?

A thập phân sang máy tính phân số tiếp tục là một công cụ chuyển đổi số thập phân (một số trong cơ sở 10) thành dạng tiếp tục của nó. Một phân số liên tục là một đại diện của một số như một phần số nguyên cộng với một loạt các phân số cho phép các biểu diễn chính xác và nhỏ gọn hơn của các số thực. Mẫu này đặc biệt hữu ích cho việc xấp xỉ các số vô lý.

---

Tại sao sử dụng số thập phân để tiếp tục máy tính phân số?

• xấp xỉ chính xác: Đó là một cách hiệu quả để gần đúng các số không hợp lý với các phân số tiếp tục hữu hạn, dễ xử lý hơn trong các tính toán.
• Ứng dụng lý thuyết số: Phân số tiếp tục được sử dụng trong lý thuyết sốPhương trình Iophantine và xấp xỉ Rễ vuông hoặc các số vô lý khác.
• Phân tích toán học: hữu ích trong việc phân tích sự hội tụ của các chuỗi hoặc chuỗi trong các trường như lý thuyết gần đúng, mật mã và toán học tính toán.
• Biểu diễn hiệu quả của các số không hợp lý: Các số không hợp lý, chẳng hạn như π hoặc E, có sự mở rộng thập phân vô hạn. Phân số tiếp tục cung cấp một cách thể hiện và xấp xỉ hiệu quả hơn và hữu ích hơn.
• Đơn giản hóa các tính toán phức tạp: Trong một số bối cảnh nhất định, các phân số tiếp tục cung cấp các biểu thức có thể quản lý hơn về các số, làm cho các tính toán liên quan đến chúng dễ dàng và hiệu quả hơn.

---

Làm thế nào để một số thập phân để tiếp tục máy tính phân số hoạt động?

1. Nhập số thập phân:
   • Nhập số thập phân bạn muốn chuyển đổi thành biểu mẫu phân số liên tục của nó.
2. Áp dụng chuyển đổi: Máy tính sẽ:
   • Chia số thập phân vào phần số nguyên và phần phân số của nó.
   • Sử dụng phần số nguyên làm thuật ngữ đầu tiên của phân số tiếp tục.
   • Lặp lại quá trình cho phần phân số, tiếp tục tìm phần số nguyên của đối ứng của phần còn lại phân số.
   • Tiếp tục cho đến khi đạt được mức độ chính xác mong muốn, hoặc phần tiếp tục được mở rộng hoàn toàn.

---

Khi nào nên sử dụng số thập phân để tiếp tục máy tính phân số?

không
• Đối với việc xấp xỉ số lượng vô lý: Khi xử lý các số không hợp lý như rễ cây, E hoặc bình phương, các phân số tiếp tục cung cấp một cách để gần đúng chúng hiệu quả hơn.
• trong tiếng khócptography: Một số thuật toán mã hóa sử dụng các phân số liên tục để phá vỡ mã hoặc trong các phương pháp thuật toán để lý thuyết số.
không
• Trong các cài đặt giáo dục: Khi nghiên cứu các hệ thống số, số không hợp lý hoặc lý thuyết về xấp xỉ, các phân số tiếp tục có thể giúp học sinh hiểu cách số thực có thể được biểu diễn dưới dạng dễ quản lý hơn.