Desimaalin jatkamiseen ja murto -osa -osin

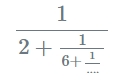
Mikä on desimaalin jatkamisen fraktiolaskurin?

A Desimaalin jatkaminen Fraktio -laskin on työkalu, joka muuntaa desimaalin lukumäärän (lukumäärä 10) sen jatkuvan fraktion -muotoksi. Jatkuva osuus on lukumäärän esitys kokonaislukuosana sekä sarjan fraktioita, jotka sallivat tarkempia ja kompakteja esityksiä todellisista numeroista. Tämä muoto on erityisen hyödyllinen irrationaalisten lukujen arvioinnissa.

Miksi käyttää desimaalia jatkamaan fraktiolaskin?

• Tarkka likiarvo: Se on tehokas tapa arvioida irrationaalisia numeroita äärellisillä jatkuvilla fraktioilla, joita on helpompi käsitellä laskelmissa.
• Numeroteorian sovellukset: Jatkuvia fraktioita käytetään lukuteoriassa irrationaalisten lukujen tutkimiseen, DIofantine -yhtälöt ja neliöjuuret tai muut irrationaaliset numerot.
• Matemaattinen analyysi: Hyödyllinen sekvenssien tai sarjojen konvergenssin analysoinnissa aloilla, kuten lähentämisteoria, kryptografia ja laskennallinen matematiikka.
• Irrationaalien tehokas esitys: Irrationaalisilla numeroilla, kuten π tai E, on ääretön desimaalilaajennukset. Jatkuvat fraktiot tarjoavat tehokkaamman ja hyödyllisemmän tavan ilmaista ja arvioida näitä lukuja.
• yksinkertaistaa monimutkaisia ​​laskelmia: Tietyissä yhteyksissä jatkuvat fraktiot tarjoavat hallittavissa olevia lukumääriä, mikä tekee niistä helpompaa ja tehokkaampaa laskelmia.

Kuinka desimaalien jatkuvaa fraktiolaskurin työtä?

1. syötä desimaalin lukumäärä:
   • Syötä desimaaliluku
2. Käytä muuntamista: Laskin:
   • Rikkoo desimaalin lukumäärän kokonaislukuosaan ja murto -osaan.
   • Käytä kokonaislukuosaa jatkuvan osan ensimmäisenä termina.
   • Toista murto -osan prosessi, jatkaen murto -jäljellä olevan vastavuoroisen kokonaisluvun löytämistä.
   • Jatka, kunnes haluttu tarkkuustaso saavutetaan tai jatkuva osa on täysin laajentunut.

---

Milloin desimaalin jatkaminen fraktiolaskurin jatkumiseen?

• lukuteoriassa: työskennellessään irrationaalisten lukujen rationaalisten likiarvojen kanssa tai diofantiinin yhtälöiden tutkimuksessa.
• irrationaalisten lukujen lähentämiseksi: Kun käsitellään irrationaalisia lukuja, kuten π-, e- tai neliöjuuria, jatkuvat fraktiot tarjoavat tavan arvioida niitä tehokkaammin.
• itkussaPtografia: Jotkut salausalgoritmit käyttävät jatkuvia fraktioita koodeiden rikkomiseen tai algoritmisiin lähestymistapoihin lukuteoriaan.
• matemaattisessa tutkimuksessa: tutkijat algebrallisen lukuteorian kaltaisilla aloilla. Käyttävät jatkuvia fraktioita ongelmien ratkaisemiseksi, jotka koskevat todellisia lukuja ja irrationaalisia vakioita.
• Koulutusympäristöissä: Kun tutkitaan numerojärjestelmiä, irrationaalisia lukuja tai likiarvojen teoriaa, jatkuvat fraktiot voivat auttaa opiskelijoita ymmärtämään, kuinka todelliset numerot voidaan edustaa hallittavissa olevassa muodossa.