Υπολογιστής εξίσωσης Arrhenius
Εισαγάγετε την τιμή και κάντε κλικ στον υπολογισμό.Αποτέλεσμα θα εμφανιστεί .
Τι είναι ένας υπολογιστής εξίσωσης Arrhenius;
Ένας υπολογιστής εξίσωσης Arrhenius είναι ένα εργαλείο που χρησιμοποιείται για τον προσδιορισμό της επίδρασης της θερμοκρασίας στις ρυθμίσεις αντίδρασης σε χημικά και βιολογικά συστήματα. Εφαρμόζει την εξίσωση Arrhenius , η οποία εκφράζει τη σχέση μεταξύ της σταθεράς ρυθμού (k) μιας αντίδρασης και της θερμοκρασίας (t):
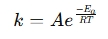
πού:
- k = σταθερά ρυθμού (1/s, 1/m · s, κλπ.)
- a = προ-εκθετικός παράγοντας (συχνότητα συγκρούσεων)
- ea = ενέργεια ενεργοποίησης (j/mol)
- r = καθολική σταθερά αερίου (8.314 j/mol · k)
- T = απόλυτη θερμοκρασία (Kelvin)
Μια αναδιαταγωγμένη μορφή χρησιμοποιείται συχνά για τη σύγκριση των ρυθμών αντίδρασης σε διαφορετικές θερμοκρασίες:
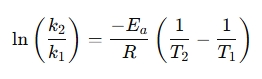
Γιατί να χρησιμοποιήσετε έναν αριθμομηχανή εξίσωσης Arrhenius;
- Προβλέπει τους ρυθμούς αντίδρασης : βοηθά τους χημικούς και τους μηχανικούς να εκτιμήσουν πόσο γρήγορα θα προχωρήσει μια αντίδραση σε διαφορετικές θερμοκρασίες.
- Καθορίζει την ενέργεια ενεργοποίησης : Υπολογίζει την ενέργεια που απαιτείται για να συμβεί μια αντίδραση.
- Βασική στη βιομηχανική χημεία : που χρησιμοποιείται στα φαρμακευτικά προϊόντα, την επιστήμη των πολυμερών και την μηχανική των υλικών.
- Υποστηρίζει περιβαλλοντικές μελέτες : Αξιολογεί τις επιδράσεις της θερμοκρασίας στις βιολογικές και ατμοσφαιρικές αντιδράσεις.
Πώς λειτουργεί ένας υπολογιστής εξισώσεων Arrhenius;
Απαιτείται είσοδος :
- Ενέργεια ενεργοποίησης (ΕΑ) σε J/mol
- θερμοκρασία (ες) σε Kelvin (T1, T2)
- Προ-εκθετικός παράγοντας (α) (προαιρετικό)
- σταθερά ποσοστού σε μία θερμοκρασία (k1) (προαιρετικό)
Επεξεργασία :
- υπολογίζει το ρυθμό constAnt (k) χρησιμοποιώντας την εξίσωση Arrhenius
- Εναλλακτικά, υπολογίζει την ενέργεια ενεργοποίησης (ΕΑ) από γνωστές σταθερές ρυθμού
- Χρησιμοποιεί λογαριθμικούς μετασχηματισμούς για συγκριτικούς υπολογισμούς.
output :
- σταθερά ρυθμού αντίδρασης (k) σε δεδομένη θερμοκρασία.
- Ενέργεια ενεργοποίησης (ΕΑ) εάν επίλυση για αυτό.
- Αλλαγή του ρυθμού αντίδρασης με θερμοκρασία.
Πότε να χρησιμοποιήσετε έναν αριθμομηχανή εξίσωσης Arrhenius;
- Στη χημεία & κινητική : Η κατανόηση του τρόπου με τον οποίο η θερμοκρασία επηρεάζει τις ταχύτητες αντίδρασης.
- Στη φαρμακευτική ανάπτυξη : Μελέτη των ποσοστών σταθερότητας και αποικοδόμησης φαρμάκων.
- Στο βιομηχανικό έλεγχο της διαδικασίας : σχεδιασμός χημικών αντιδράσεων ευαίσθητων στη θερμοκρασία.
- Στην περιβαλλοντική επιστήμη : πρόβλεψη των ποσοστών αντίδρασης στις κλιματικές μελέτες και στοχημεία με φόστη.
Σας βοήθησε αυτή η Αριθμομηχανή;
Ευχαριστώ για τα σχόλια


Αναζήτηση αριθμομηχανής
Εξερευνήστε χιλιάδες δωρεάν αριθμομηχανές που εμπιστεύονται εκατομμύρια σε όλο τον κόσμο.